摘 要
在点的合成运动问题中,动点和动系的选择是解题的关键。本文梳理了相关文献中关于动点和动系的选取原则和方法,根据近年来出现的一些新题型增加了相关内容并进行分类,总结得出了选取动点的一套更全面和直观的方法,即动点为质点、不计尺寸的运动构件、不变的接触点、圆心、铰链及辅助物体等六种类型。同时,对于一些特殊类型的题目进行了讨论,分析了解题过程中出现的常见错误,并给出了更恰当的解答方法。研究结果可为青年教师及学生提供有益的参考。
关键词 合成运动;动点;方法;分类
Abstract In the resultant motion problem of point, the selection of moving point and moving coordinate system is the key to solve the problem. This paper introduces the selection principles and methods of moving point and moving coordinate system in relevant literature, and adds some supplementary contents according to some new types of questions in recent years, and summarizes a set of more comprehensive methods for the selecting of moving point within six types of questions, where the moving point can be particle, moving member regardless size, constant contact point, center of the circle, hinge and auxiliary objects. At the same time, some special types of problems are discussed, and the common errors in solving problems are analyzed, and more appropriate solutions are provided. The results can be the beneficial reference for young teachers and students.
点的合成运动是理论力学课程中运动学部分的重点内容。动点动系的分析方法是解决机构中各构件间运动关系的行之有效的方法。总结起来,就是要理解一点、两系、三运动的概念,即动点,动参考系、定参考系,绝对运动、相对运动和牵连运动,而动点和动系的选择决定了解题的难易程度甚至成败。关于动点和动系的选取原则,已有较多文献发表[1-5],陈奎孚等[6]进行了总结和讨论,认为最重要的两条原则是:1)动点不能选在固结动系的刚体上;2)动点的相对运动简单。关于动点的具体选取方法也有较多文献进行了讨论[2, 7-13],陈奎孚等[12, 13]总结了动点动系选取方法的五“相”形,提出了一些新的方法,并对一些问题进行了深入的讨论[14],各文献各有特点,但所列方法仍不尽全面。随着近年来出现的一些新题型,特别是一些高校的考研题目,又为动点的选取提出了一些新的问题,因此有必要再进行总结和归类,给出一套更加完善和直观的动点选取方法。本文基于现有文献,并根据近年来出现的一些新题型对动点的选取方法进行了归纳和总结,得出了针对六种不同类型问题的动点选择方法。
1 动点的选取方法
1.1 质点间的相对运动问题
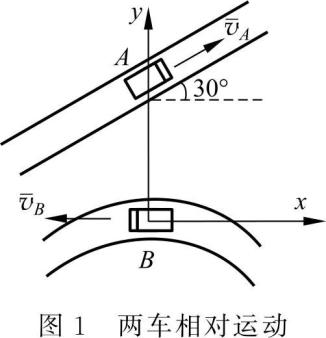
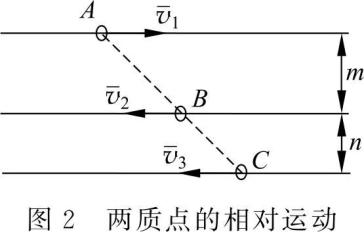
此类型是两个互不相连物体的相对运动问题,可将物体看成质点。则可选择其中一个为动点,另一个为动系。如图 1 所示,已知两车的速度,求 A 车上的人看到的 B 车的速度。此时可选 B 车为动点,像不计尺寸的滑块一样。图 2 题中,已知质点 A 、B 的速度,且三个质点的连线始终保持为一条直线,求质点 C 的速度,则选择质点 C 为动点,分别选择其余两质点作为动系即可。
1.2 刚体的相对运动问题
1)套筒、滑块或小圆环
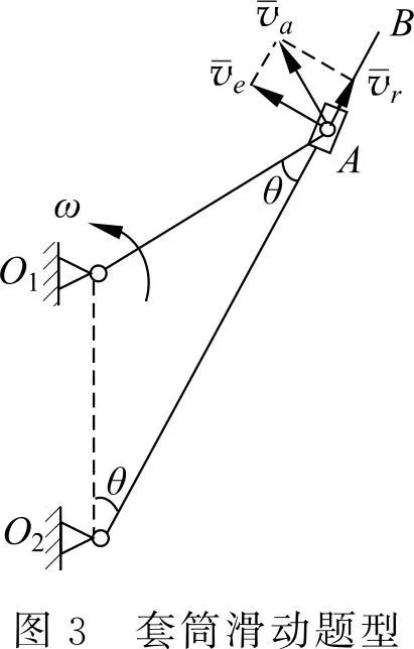
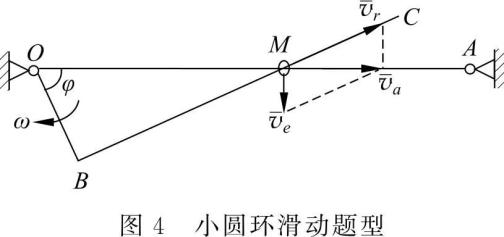
题目中出现了具有明显的可以不计尺寸的运动物体。此类型是运动机构中有套筒、滑块或小圆环相对于另一个刚体运动,则选择它为动点,动系固结在其相对运动的刚体上。如图 3 所示为套筒滑动问题,选择套筒 A 为动点,动系固结在 O 2B 杆上。图 4 为小圆环滑动题型,则选择小圆环 M 为动点,动系固结在曲杆 OBC 上。各题速度平行四边形如图中所示。
2)不变的接触点
此类型是两个相互接触刚体的相对运动问题,其中一个刚体的接触点始终与另一个刚体接触,则该刚体上的接触点选择为动点,动系固结在另一个刚体上。如图 5(a)所示,选择 AB 杆上的 A 点作为动点,动系固结在凸轮 O 上,图 5(b)则选择 OA 杆上的 A 点作为动点,速度平行四边形如图所示。
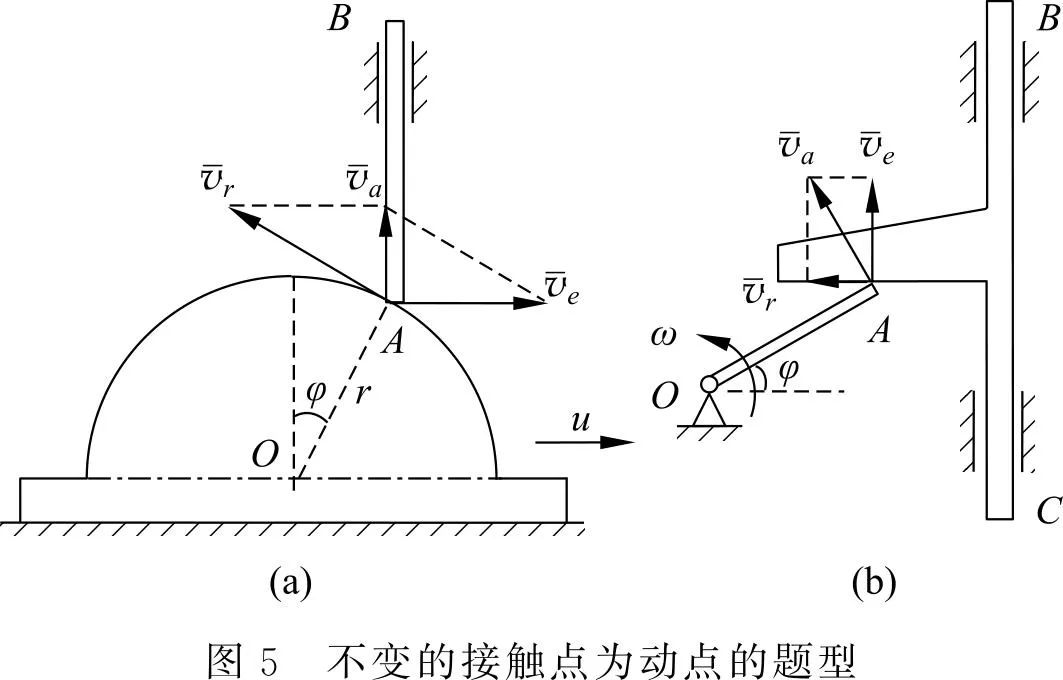
此类接触类型的题目,若动点选择反了,即选择了变化的接触点作为动点,则相对轨迹不明确,使得加速度分析困难或出错。
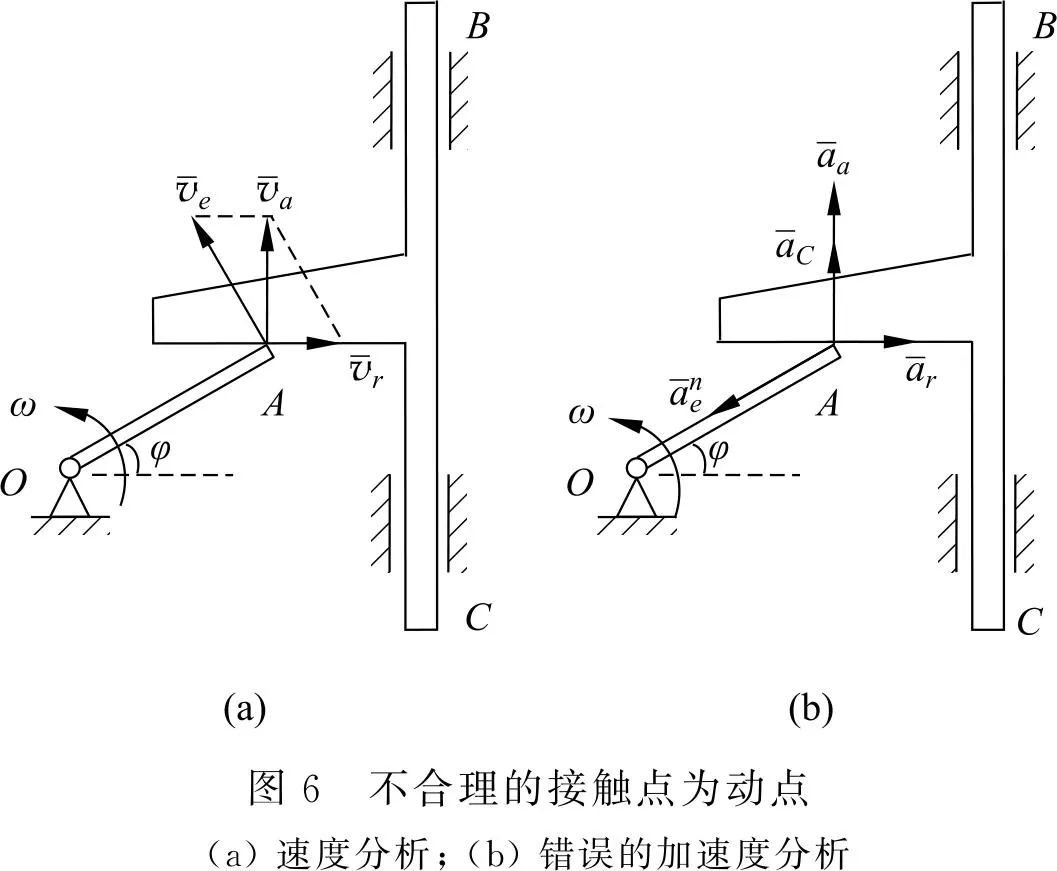
如图 6 所示,如果选择平板上的接触点作为动点,速度分析见图 6(a),所得结果正确,其原因是相对轨迹虽然是曲线,但该点此时的相对轨迹的切线方向正好是水平方向[3],因此相对速度确实是水平方向。
如果以杆上的接触点为动点,其相对加速度方向按水平方向就是错误的了,并且此时还会出现科氏加速度,因此选择接触点不合理,会导致解题困难甚至错误。如图 6(b)所示,可解出平板 BC 的加速度,其方向向上。然而其加速度实际方向是向下的,因此解答是错误的。
原因在于你视OA杆的O点会动,但是实际O点不是一个套在杆上的滑块上的质点,无法滑动
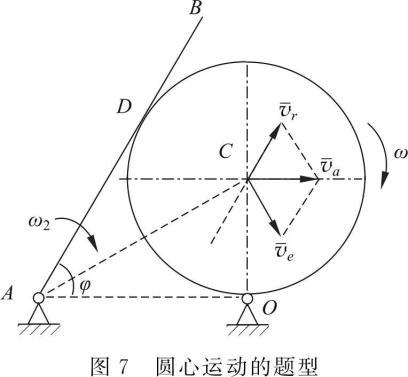
3)圆心
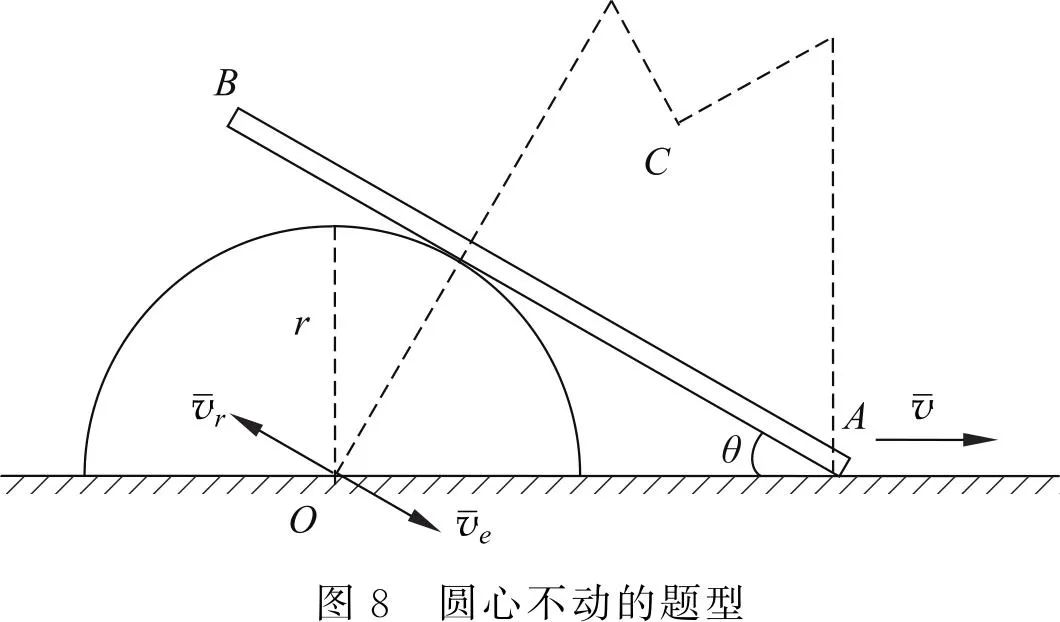
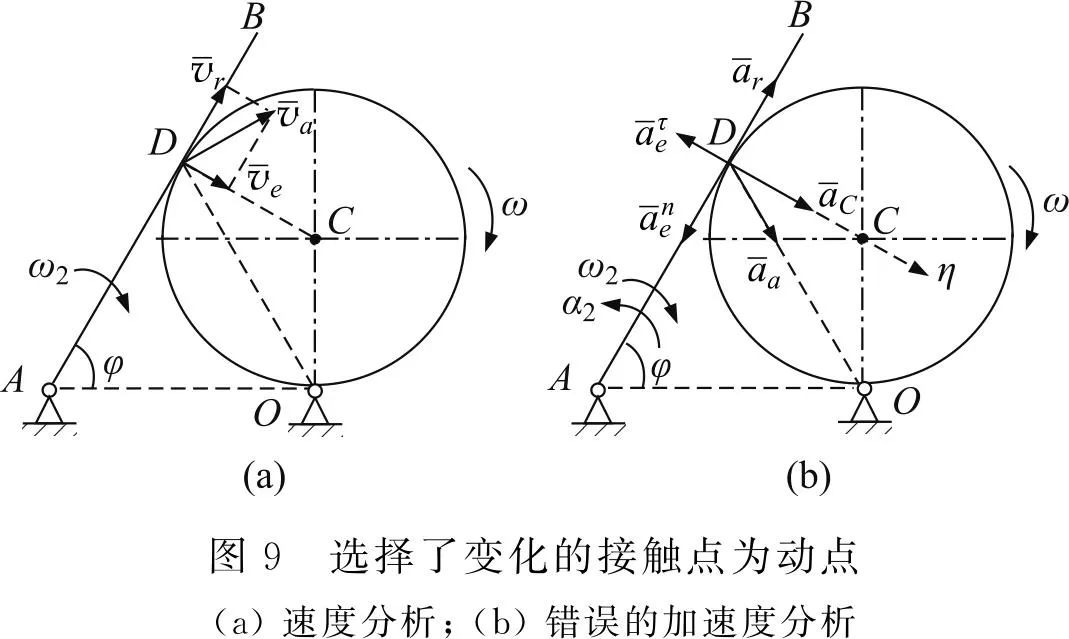
在一些题目中,虽然也是有两个刚体接触的相对运动,但两个刚体的接触点都是时刻发生变化,此时不宜再选择接触点作为动点,此时的情况一般会有一个刚体具有圆心,则选择圆心为动点,动系固结在另一个刚体上。如图 7 所示,选择圆心 C 为动点,动系固结在 AB 杆上,相对运动是平行于 AB 杆的直线运动,速度和加速度分析都简单、清晰。图 8 则是 AB 杆在固定的半圆上滑动的问题,此时虽然圆心 O 不动,但仍然可选择圆心 O 作为动点,动系固结在 AB 杆上。可见,动点相对定参考系不一定必须要运动。
对于图 7 的题目,很多学生非常容易出现错误,主要在于选择了接触点 D 为动点。如图 9 所示,选择圆盘上的接触点 D 为动点,动系固结在 AB 杆上,错误地认为相对运动是沿着 AB 方向的滑动。速度分析见图 9(a),仍然可得出 AB 杆正确的角速度,原因也是此时的相对轨迹的切线方向正好是沿 AB 方向,但加速度分析如图 9(b)所示,则得不到正确的答案。可见,这类题目的动点选择不合适,速度一般能算对,但加速度分析将非常困难。
4)两杆的连接铰链
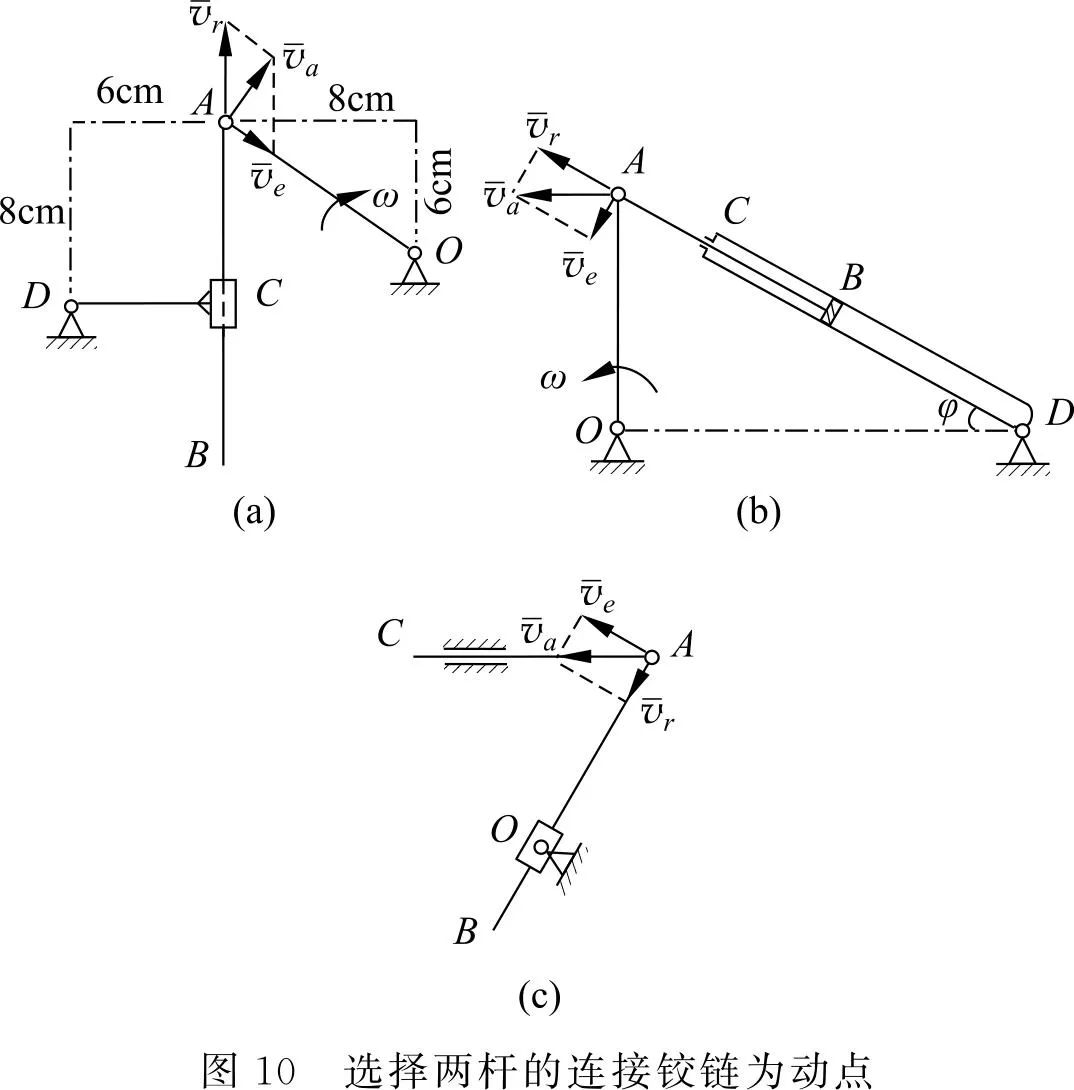
还有一些题目,特别是一些稍难的题目,没有前述几种类型的情况可作为动点,此时一般会有两杆的连接铰链,则选择该铰链作为动点可顺利的解出答案。如图 10(a)所示,求 CD 杆的角速度和角加速度。看似选择套筒 C 作为动点,属于前述1)的类型,但这样做速度分析就已经解不出答案,加速度就更不可解。此题只能选择曲柄的端点 A 作为动点,动系固结在 CD 杆上,则十分简单。图 10(b)是一道运动学综合题,求活塞 B 的速度和加速度。若选择活塞 B 为动点,误以为是属于1)的类型,将解不出答案,此时需选 A 为动点,动系固结在气缸 CD 上才可顺利解题。图 10(c)没有曲柄,但仍然选择两杆的连接铰链 A 为动点,动系固结在套筒 O 上,则问题将大为简化。
5) 增加辅助物体作为动点或动系
还有一些题目,很难看出明确的动点,此时不妨增加辅助物体作为动点或动系[2,7]。如图 11(a)所示,已知两杆的平动速度,求它们的交点的速度,此时不妨在交点上假想的添加一个小圆环 E,则其速度即为所求,将问题变成了1)的类型。此题需要以小圆环 E 为动点,分别以两杆为动系进行两次速度合成分析,从而解出答案。
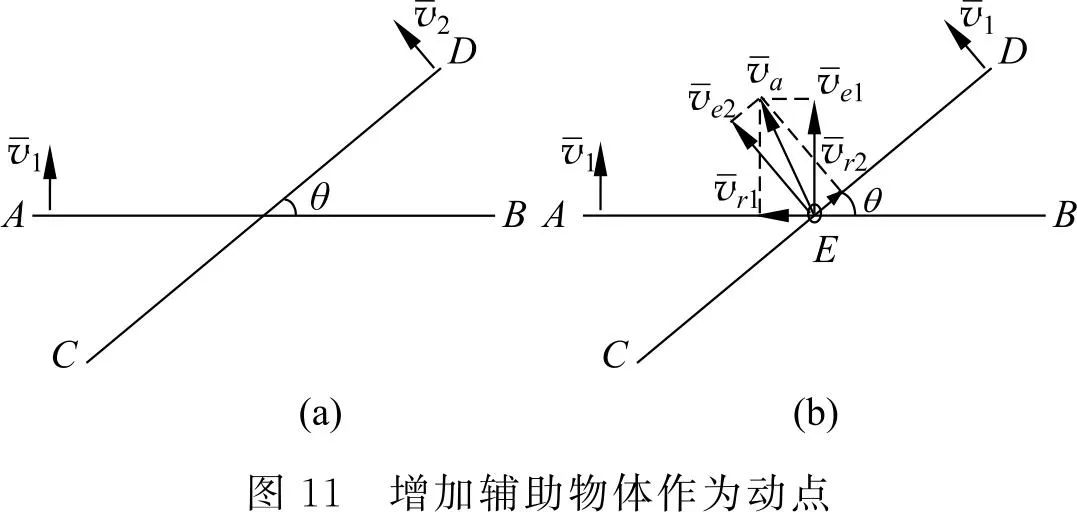
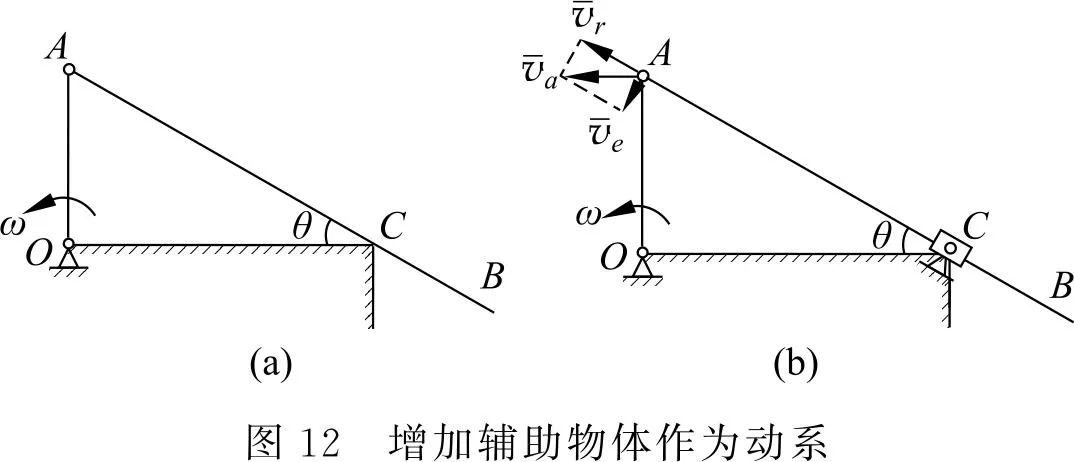
图 12(a)题目看上去不是点的合成运动的问题,求 AB 杆的角速度和角加速度。此时考虑选择曲柄端点 A 为动点,但是动系固结到哪里呢?由于 AB 杆始终与桌角 C 点接触,那么不妨假想在 C 点有一个套筒,见图 12(b),将动系固结在套筒 C 上,则三种运动的分析就非常简单,此题可迎刃而解。
2 结语
点的合成运动是运动学部分中的重点内容,合理的选择动点将是解题的关键所在。根据现有文献和近年来出现的一些新题型,将动点的具体选取方法总结为六种类型问题,即动点为质点、不计尺寸的运动构件、不变的接触点、圆心、铰链及辅助物体,该结论为选取动点的一套更为全面和直观的方法。同时,还对一些解题错误的原因进行了分析,给出了正确的解答方法。本文的方法将有利于快速确定动点和动系,从而为解题带来便利,研究结果可作为青年教师讲课及学生学习本章内容时的有益参考。
参考文献
[1]李淑堃. 关于动点动系的选择原则[J]. 力学与实践, 1985(5): 54-57.
LI S K. On the selection principles of moving point and moving coordinate system[J]. Mechanics in Engineering, 1985(5): 54-57. (in Chinese)
[2]薛克宗. 动点动系的选择方法与相对运动轨迹的几何性质[J]. 力学与实践, 1986(1): 47-49.
XUE K Z. The selection methods of moving point and moving coordinate system and geometric properties of relative motion[J]. Mechanics in Engineering, 1986(1): 47-49. (in Chinese)
[3]李佩春, 任贵斌, 彭祝. 对“关于动点动系选择原则”一文的讨论[J]. 力学与实践, 1987(1): 40-46.
LI P C, REN G B, PENG Z. Discussion on the article “On the selection principles of moving point and moving coordinate system”[J]. Mechanics in Engineering, 1987(1): 40-46. (in Chinese)
[4]冯立富. 动点和动系的选取原则和方法[J]. 力学与实践, 1987(5): 51-52.
FENG L F. The selection principles and methods of moving point and moving coordinate system[J]. Mechanics in Engineering, 1987(5): 51-52. (in Chinese)
[5]吴云存. 动点动系选择的唯一准则[J]. 湖北汽车工业学院学报, 2000, 14(4): 8-12.
WU Y C. The only selection principles of moving point and moving coordinate system[J]. Journal of Hubei Institute of Automobile Industry, 2000, 14(4): 8-12. (in Chinese)
[6]陈奎孚, 王建立. 动点—动系选择中若干问题的商榷[J]. 邢台职业技术学院学报, 2008, 25(3): 1-2.
CHEN K F, WANG J L. Some comments on selecting moving point and moving coordinate[J]. Journal of Xingtai Polytechnic College, 2008, 25(3): 1-2. (in Chinese)
[7]王小岗. 论点的复合运动中动点、动系的选择原则和方法[J]. 青海大学学报, 1994, 12(1): 10-14.
WANG X G. The selection principles and methods of moving point and moving coordinate system in the resultant motion problem of point[J]. Journal of Qinghai University, 1994, 12(1): 10-14. (in Chinese)
[8]干为民. 点作合成运动时动点、动系、定系选择方法的讨论[J]. 常州工业技术学院学报, 1994, 7(4): 42-48.
GAN W M. The selection methods of moving point, moving coordinate system and fixed coordinate system in the resultant motion problem of point[J]. Journal of Changzhou Institute of Technology, 1994, 7(4): 42-48. (in Chinese)
[9]李之祥. 论点的合成运动中动点、动系的选择与解题难易的关系[J]. 昆明冶金高等专科学校学报, 1995, 11(1): 50-55.
LI Z X. On the relationship between the selection of moving point, moving coordinate system in the resultant motion problem of point and the difficulty of solving problems[J]. Journal of Kunming Metallurgical College, 1995, 11(1): 50-55. (in Chinese)
[10]张东峰, 陈晓峰. 关于点的合成运动中动点的选取[J]. 高等理科教育, 2004(2): 87-90.
ZHANG D F, CHEN X F. The selection of moving point in the resultant motion problem of point[J]. Higher Science Education, 2004(2): 87-90. (in Chinese)
[11]王晨. 点的合成运动中动点和动系的选择[J]. 山西建筑, 2004, 30(24): 28-29.
WANG C. The selection of moving point and moving coordinate system in the resultant motion problem of point[J]. Shanxi Construction, 2004, 30(24): 28-29. (in Chinese)
[12]陈奎孚, 王建立. 合成运动分析的五“相”型[J]. 邢台职业技术学院学报, 2009, 26(1): 1-5.
CHEN K F, WANG J L. Five classes of composite movement analysis[J]. Journal of Xingtai Polytechnic College. 2009, 26(1): 1-5. (in Chinese)
[13]陈奎孚. 理论力学精细辅导[M]. 北京: 清华大学出版社, 2018: 166-181.
[14]陈奎孚, 姚海蓉, 张云文. 相切型传递的加速度表现[J]. 物理与工程, 2018, 28(2): 29-35.
CHEN K F, YAO H R, ZHANG Y W. The acceleration manifest of the tangent-type transmission[J]. Physics and Engineering, 2018, 28(2): 29-35. (in Chinese)
基金项目: 河北省教学改革研究与实践项目(2019GJJG077)。
通讯作者: 余为,男,燕山大学副教授,主要从事轻质多孔功能复合材料的研究工作,yuweichn@163.com。
引文格式: 余为, 郝颖. 点的合成运动中动点的选取方法分类与讨论[J]. 物理与工程, 2022, 32(2): 36-39, 49.
Cite this article: YU W, HAO Y. Discussion and classification for the selection methods of moving point in resultant motion[J]. Physics and Engineering, 2022, 32(2): 36-39, 49. (in Chinese)