引言:大学物理PPT上证明过程相当于没有,而且很多PPT都不从定性的角度去告诉你科里奥利力的来源或者说当年科里奥利是如何察觉到这个力的
质点下的分析
建模
假设
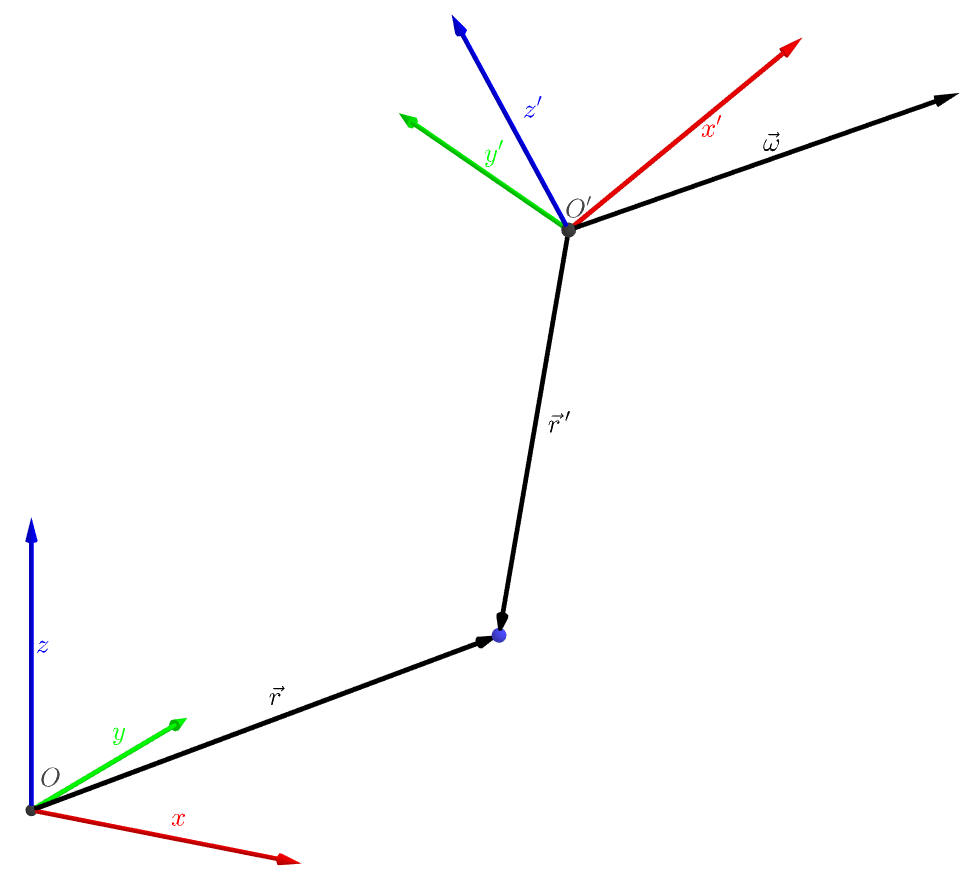
设有二参考系 S 与 S'。
S 以 O 为原点,\vec{\mathbf{i}}、\vec{\mathbf{j}}、\vec{\mathbf{k}} 为坐标基。
S' 以 O' 为原点,\mathbf{\vec{i}'}、\mathbf{\vec{j}'}、\mathbf{\vec{k}'} 为坐标基,相对 S 以角速度 \boldsymbol{\omega} 旋转。
某点在 S 的径矢为 \vec{\mathbf{r}},在 S' 的径矢为 \mathbf{\vec{r}'}。
方法一:正交矢量证明
分析
目的
求解:点在两个坐标系下的加速度之间的关系式

求解
1. 求解径矢关系
图像依据:绝对位移=参考位移+相对位移
得:\mathbf{\vec{r}} = \mathbf{\vec{OO'}} + \mathbf{\vec{r'}} \tag {1-1}
\because \mathbf{\vec{r}'} 在 \mathbf{S'} 的坐标为 (x', y', z') \therefore\mathbf{\vec{r}'}在O'系下的正交化表达
得: \mathbf{\vec{r}'} = x' \mathbf{\vec{i}'} + y' \mathbf{\vec{j}'} + z' \mathbf{\vec{k}'} \tag{1-2}

2. 求解速度关系
位矢恒等式左右微分:动得点绝对速度=动系参考速度+动点相对速
得右式\frac{d\vec{r}}{dt} = \frac{d\vec{OO'}}{dt} + \frac{d\vec{r'}}{dt}\tag{2-1}
对其进行化简,过程如下
\begin{align*}
\frac{d\vec{r}}{dt} &= \frac{d\vec{OO'}}{dt} + \frac{d\vec{r'}}{dt} \\
&\because \mathbf{\vec{r}'} = x' \mathbf{\vec{i}'} + y' \mathbf{\vec{j}'} + z' \mathbf{\vec{k}'} \therefore d{\vec{r}'}=d(x' \mathbf{\vec{i}'} + y' \mathbf{\vec{j}'} + z' \mathbf{\vec{k}'})\\
&= \frac{d\vec{OO'}}{dt} + (\frac{dx’}{dt} \vec{i'} + x' \frac{d\vec{i'}}{dt} + \frac{dy'}{dt} \vec{j'} + y' \frac{d\vec{j'}}{dt} + \frac{dz'}{dt} \vec{k'} + z' \frac{d\vec{k'}}{dt}) \tag{2-2}
\end{align*}
回忆对比:以平动参考系中为基准系分析的时候,参考速度\frac{d{\vec{i}'}}{dt}、\frac{d{\vec{j}'}}{dt}、\frac{d{\vec{k}'}}{dt}都是0的,因为相对参考系的速度就是绝对参考系的速度,相对参考系不相对于原坐标系发生位矢变化。
假设解释法:假设质点不发生相对运动,相对参考系和绝对参考系间就没有位矢的变化,而旋转系为基准系下的参考系却不是这样,即使质点不发生相对运动,绝对参考系与相对参考系就会发生位移矢的变化
恒等式解释: 以步进分析思想因此我们可以如下步步分析
绝对对位移=参考位移+相对位移-->相对参考系对于绝对参考系的位移矢变化式-->求解质点相对于参考系位移矢的表达式
- 平动视角下第二个步为常值,因此一阶二阶导为0,第三个步为与时间t有关的函数
- 旋动视角下第二个步为与时间t有关的函数,第三个步也为与时间有关的函数
title:思考
**出现$\frac{dx'}{dt},\frac{dy'}{dt},\frac{dz'}{dt}$的原因**
1. $x'$实际为$x'(t)$代表动点在相对坐标系下$x'$轴上的位移投影,其他轴同理
2. 本身$\vec{i}'$便是$\vec{i}'(t)$的变量,只是书写的过程中略去了
**为何不直接用$\vec{x}'$证明?**
3. 利用标量X矢量=矢量恒等证明,若你以$\vec{x}'$去证明的话,要比拆解其为$x'\vec{i}$的证明方法要麻烦
**从$V_a=V_e+V_r$出发却多推出来个科式速度,违背定理么?**
4. 合理,我们是从恒等式出发,经过恒等微分化得到的此式,对于前式也是以平动参考系未视角下经过位矢恒等微分得到的。两个推理逻辑是一样的,理解此点方能打破公式的刻板记忆
**注意:第一点是推导关键理解点,若你视$x'$为常量,则它不对相对参考系发生相对运动了**
2.1 求解O’系基元上的速度元
解释:之所以要求解这个,是因为对于一个确定的角速度,给定一位矢,它就能在这个位矢上产生线速度量。
其实更确切的说,在动点相对于动系运动时候,除了动点自己的相对位移导数产生的速度,还有绝对坐标系给他带来的附加速度,也就是说这个相对坐标系的相对速度受到绝对坐标系的影响!
O系\vec\omega在O'系下对其x'产生的单位相对速度
\frac{d\mathbf{\vec{i}'}}{dt}(S) = \boldsymbol{\vec\omega} \times \mathbf{\vec{i}'} \tag{3-1}
O系\vec\omega在O'系下对其y'产生的单位相对速度
\frac{d\mathbf{\vec{j}'}}{dt}(S) = \boldsymbol{\vec\omega} \times \mathbf{\vec{j}'} \tag{3-2}
O系\vec\omega在O'系下对其z'产生的单位相对速度
\frac{d\mathbf{\vec{k}'}}{dt}(S) = \boldsymbol{\vec\omega} \times \mathbf{\vec{k}'} \tag{3-3}
title:对$\vec{v}=\vec\omega \times \vec{r}$新思考
1. 角速度可以在任意方向向量上产生的速度矢积,数值交给外积运算决定
2. 原坐标系在动系三个坐标轴上产生的单位速度向量
2.2 回代换元求速度
带入(3-1)(3-2)(3-3)式到(2-2)式可得
\begin{align*}
\frac{d\vec{r}}{dt}&= \frac{d\vec{OO'}}{dt} + \frac{d\vec{r'}}{dt}\\
&= \frac{d\vec{OO'}}{dt} + (\frac{dx'}{dt} \vec{i'} + x \boldsymbol{\vec\omega} \times \vec{i'} + \frac{dy'}{dt} \vec{j'} + y' \boldsymbol{\vec\omega} \times \vec{j'} + \frac{dz'}{dt} \vec{k'} + z' \boldsymbol{\vec\omega} \times \vec{k'}) \tag{4-1}
\end{align*}
\because \therefore\vec\omega\vec{r}'=\vec\omega(x'\vec{i}'+y'\vec{j}'+z'\vec{k}')
\therefore\frac{d\vec{\mathbf{r}}}{dt}(S) = \frac{d\vec{\mathbf{OO'}}}{dt}(S) + \frac{d\vec{\mathbf{r'}}}{dt}(S') + \vec{\boldsymbol{\omega}} \times \vec{\mathbf{r'}} \tag{4-2}
记 $\frac{d\mathbf{r}}{dt}(S)$ 为 $\mathbf{\vec{v_a}}$,$\frac{d\mathbf{OO'}}{dt}(S)$ 为 $\mathbf{\vec{v_e}}$,$\frac{d\mathbf{e'}}{dt}(S')$ 为 $\mathbf{\vec{v_r}}$,于是有
\mathbf{\vec{v_a}} = \mathbf{\vec{v}}_{e} + \mathbf{\vec{v_r}}' + \boldsymbol{\vec\omega} \times \mathbf{\vec{r}'}\tag{4-3}
title:技巧学习
1. 可以看到,参考系的速度矢量微分始终都是没有正交化表达的,因为本身它就表示$\vec{a_e}$所以不需要进行正交分解
2. 而
2.2 回代换元求速度
带入(3-1)(3-2)(3-3)式到(2-2)式可得
\begin{align*}
\frac{d\vec{r}}{dt}&= \frac{d\vec{OO'}}{dt} + \frac{d\vec{r'}}{dt}\\
&= \frac{d\vec{OO'}}{dt} + (\frac{dx'}{dt} \vec{i'} + x \boldsymbol{\vec\omega} \times \vec{i'} + \frac{dy'}{dt} \vec{j'} + y' \boldsymbol{\vec\omega} \times \vec{j'} + \frac{dz'}{dt} \vec{k'} + z' \boldsymbol{\vec\omega} \times \vec{k'}) \tag{4-1}
\end{align*}
\because \therefore\vec\omega\vec{r}'=\vec\omega(x'\vec{i}'+y'\vec{j}'+z'\vec{k}')
\therefore\frac{d\vec{\mathbf{r}}}{dt}(S) = \frac{d\vec{\mathbf{OO'}}}{dt}(S) + \frac{d\vec{\mathbf{r'}}}{dt}(S') + \vec{\boldsymbol{\omega}} \times \vec{\mathbf{r'}} \tag{4-2}
记\frac{d\mathbf{r}}{dt}(S)为 \mathbf{\vec{v_a}},\frac{d\mathbf{OO'}}{dt}(S) 为 \mathbf{\vec{v_e}},\frac{d\mathbf{e'}}{dt}(S') 为 \mathbf{\vec{v_r}},于是有下式成立
\mathbf{\vec{v_a}} = \mathbf{\vec{v}}_{e} + \mathbf{\vec{v_r}}' + \boldsymbol{\vec\omega} \times \mathbf{\vec{r}'}\tag{4-3}
title:技巧学习
1. 可以看到,参考系的速度矢量微分始终都是没有正交化表达的,因为本身它就表示$\vec{a_e}$所以不需要进行正交分解
2. 而
3. 加速度的推导
解释:如果你尝试对上式速度进行微分求解加速度你就会发现科式速度项非常棘手,因为你不知道该项关于t的具体表达式,不妨我们回到(4-1)位移表达式连续进行两次导来看看结果
\begin{align*}
\frac{d^2\mathbf{r}}{dt^2}(S) = & \frac{d^2\mathbf{OO'}}{dt^2}(S) + \frac{d^2x}{dt^2} \mathbf{i'} + 2 \frac{dx}{dt} \boldsymbol{\omega} \times \mathbf{i'} + x \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{i'} \\
& + x \boldsymbol{\omega} \times \frac{d\mathbf{i'}}{dt}(S) + \frac{d^2y}{dt^2} \mathbf{j'} + 2 \frac{dy}{dt} \boldsymbol{\omega} \times \mathbf{j'} + y \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{j'} \\
& + y \boldsymbol{\omega} \times \frac{d\mathbf{j'}}{dt}(S) + \frac{d^2z}{dt^2} \mathbf{k'} + 2 \frac{dz}{dt} \boldsymbol{\omega} \times \mathbf{k'} + z \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{k'} \\
& + z \boldsymbol{\omega} \times \frac{d\mathbf{k'}}{dt}(S)
\end{align*}
注意:$x,y,z$与$i',j',k'$一样都是关于时间$t$的函数,区别在于一个是标量函数一个是矢量函数,所以有乘积微分项
4. 化简分析

\frac{d^2\mathbf{r}}{dt^2}(S) = \frac{d^2\mathbf{OO'}}{dt^2}(S) + \frac{d^2\mathbf{r'}}{dt^2}(S') + 2 \boldsymbol{\omega} \times \frac{d\mathbf{r'}}{dt}(S') + \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{r'} + \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r'})
记 $\frac{d2\mathbf{r}}{dt2}(S)$ 为 $\mathbf{a}$,$\frac{d2\mathbf{OO'}}{dt2}(S)$ 为 $\mathbf{a}{S'}$,$\frac{d2\mathbf{r'}}{dt2}(S')$ 为 $\mathbf{a}'$,$\frac{d\boldsymbol{\omega}}{dt}(S)$ 为 $\frac{d\boldsymbol{\omega}}{dt}$,于是有:
\mathbf{a} = \mathbf{a}_{S'} + \mathbf{a}' + 2 \boldsymbol{\omega} \times \mathbf{v}' + \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{r'} + \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r'})
即:绝对加速度=参考加速度+相对于参考系的加速度+科式加速度+(线加速度+离心加速度)
==注意:理论力学第七章用到的科里奥力模型里的参考加速度就是离心加速度+角加速度,一般都是不引入角加速度变量**==
结论
绝对加速度=参考加速度+相对于参考系的加速度+科式加速度+(线加速度+离心加速度)
完善
赋予绝对参考系加速度
\mathbf{F} = m \mathbf{a} = m \mathbf{a}_{S'} + m \mathbf{a}' + 2m \boldsymbol{\omega} \times \mathbf{v}' + m \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{r'} + m \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r'})
移项后得到:
\mathbf{F} - m \mathbf{a}_{S'} - 2m \boldsymbol{\omega} \times \mathbf{v}' - m \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{r'} - m \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r'}) = m \mathbf{a}'
因此可以将惯性力写出
来:
[math:0]\mathbf{F}_I = -m \mathbf{a}_{S'} - 2m \boldsymbol{\omega} \times \mathbf{v}' - m \frac{d\boldsymbol{\omega}}{dt} \times \mathbf{r'} - m \boldsymbol{\omega} \times (\boldsymbol{\omega} \times \mathbf{r'})[/math:0]
方法二:纯矢量证明
方法三:矩阵证明
科里奥利力的推导 - 知乎 (zhihu.com)
质点系下的分析